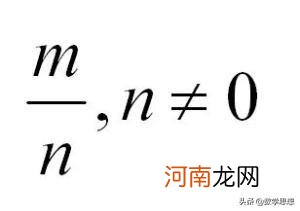
0是不是有理数，什么是有理数？

文章插图
前面，我们在《无理数的认识》那一讲中曾经谈到，人们知道无理数已经有很长的历史了，可是要清晰地表达无理数却是相当困难的。事实上，要能够清晰地表达无理数，首先要变换有理数的表达方式。我们曾经称可以表示为m/n的数为有理数，其中m,n∈Z，n≠0 。当然，在这个基础上是可以定义无理数的，比如，称不能表示为分数形式的数为无理数，但是这个定义实在是很难判断，特别是与数轴之间很难建立起对于关系。因此，我们首先建立能与数轴对应的有理数的定义，这就需要用小数来定义有理数。那么，分数与小数之间有什么关系呢？一个(0,1)上的小数可以一般地表示为
A=0.a1a2…ap （1）
或者
B=0.a1a2…ap… （2）
两种形式，其中a1，a2，…，ap是取值0或者1到9的自然数。我们称A为有限小数，B为无限小数。可以发现，有的分数可以化为有限小数，有的分数虽然不能化为有限小数，但是去能化为循环的无限小数，比如，
1/2=0.5
1/3=0.333…
1/6=0.1666…
1/7=0.142857142857…
等等。这个表达是不是具有一般性呢？也就是说，是否“所有的分数都可以化为有限小数或无限循环小数”呢？答案是肯定的，我们来证明这个结论。
考虑分数m/n，不失一般性，我们假定m<n 。如果这个分数能够化为有限小数，那么，结论成立。如果不能化为有限小数，用m除以n必有余数，并且这个余数只能取1和n-1之间的整数。由除法的运算法则，有余数后的除法都是加0填位，因为运算规律是一样的，因此，最多n次运算后，某个余数必然还要出现第二次，并且以后都是以周期形式出现，这就形成了循环小数。于是我们证明了：所有的分数都可以化为有限小数或者无限循环小数。
那么，现在是否就可以用“有限和无限循环小数”来定义有理数呢？为时过早，如果要对一个已有的定义构造一个新的定义，那么，这个新的定义的前提与结论必须是充分必要的，因为只有这样才能保持定义的等价性，为此，我们还需要证明“有限小数或者无限循环小数都能化为分数” 。由（1）式，一个有限小数可以写为
A=a1/10 a2/102 … ap/10p
这显然可以对应于一个分数。一个无限循环小数可以分为两部分，一部分是前面有限个（可以是0个）不循环项，然后是无限个循环项，不失一般性，我们假定无限循环小数是由循环项构成的，这样，（2）式可以写为
B=0.a1a2…ap a1a2…ap a1a2…ap…
=a1(1/10 1/10q 1 1/102q 1 …) … aq(1/10q 1/102q …)
=C(1 1/10q 1/102q …)
其中，C=0.a1a2…ap，括号中是一个等比级数，公比是1/10q，其中q≧1 。用sn表示前n项部分和，即
sn=1 1/10q 1/102q … 1/10nq
=[1-1/10q(n 1)]/(1-1/10q)
因为1/10q<1，容易验证当n→∞时sn→1/1-1/10q，因此
B=0.a1a2…ap/1-1/10q
【0是不是有理数，什么是有理数？】这显然是一个分数，因而是一个有理数。
现在，我们可以给出有理数的基于小数的定义了：“有理数是有限小数或者无限循环小数” 。进而可以得到无理数的定义：“无理数是无限非循环小数” 。在这个基础上，可以得到实数的定义：“有理数和无理数统称为实数” 。我们用R表示实数的全体所构成的集合。我们终于把实数刻画清楚了，并且还知道实数是与数轴上的点对应的。
我们还需要通过建立实数的运算来检验这种实数的定义是否合适。显然，这个运算是以有理数的四则运算为基础的，而重点是解决无理数的运算。以√2与√3的运算为例，下面是利用计算器计算的结果。由√2=1.4142135…和√3=1.7320508…，可以得到